Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AB = a căn bậc hai 5, AC = a
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, \[AB = a\sqrt 5 \], AC = a.. Cạnh bên SA = 3a và vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABC.
Trả lời:
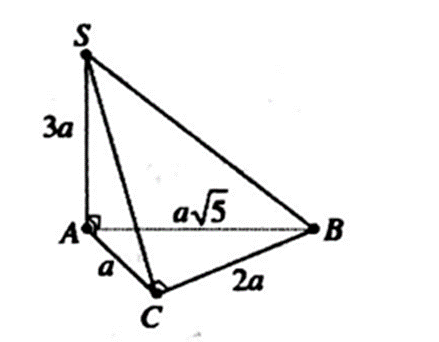
Vì DABC vuông nên áp dụng định lý Py-ta-go, ta có:
\[CB = \sqrt {A{B^2} - A{C^2}} = \sqrt {5{a^2} - {a^2}} = 2a\]
Diện tích đáy \[{S_{\Delta ABC}} = \frac{1}{2}.a.2a = {a^2}\]
Thể tích khối chóp là:
\[{V_{S.ABC}} = \frac{1}{3}.{S_{\Delta ABC}}.SA = \frac{1}{3}.{a^2}.3a = {a^3}\]
Vậy thể tích của khối chóp S.ABC là a3.


