Cho hàm số f(x)=ax^4+bx^3+cx^2+dx+e (a khác 0)

Cho hàm số $f\left(x\right)=a{x}^4+b{x}^3+c{x}^2+dx+e$. Biết rằng hàm số $f\left(x\right)$  có đạo hàm là $f\text{'}\left(x\right)$ và hàm số $y=f\text{'}\left(x\right)$  có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?

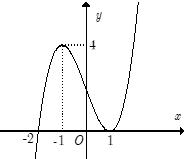
A. Trên $\left(-2;1\right)$  thì hàm số $f\left(x\right)$  luôn tăng. 

B. Hàm $f\left(x\right)$  giảm trên đoạn $\left[-1;1\right]$ . 

C. Hàm $f\left(x\right)$  đồng biến trên khoảng $\left(1;+\infty \right)$ . 

Dựa vào đồ thị của hàm số $y=f\text{'}\left(x\right)$ ta thấy:

$f\text{'}\left(x\right)>0$ khi $\left[\begin{array}{l}-2<x<1\\ x>1\end{array}\right.\stackrel{}{\to }$ $f\left(x\right)$   đồng biến trên các khoảng $\left(-2;1\right)$ , $\left(1;+\infty \right)$  .

Suy ra A và C đều đúng.

$f\text{'}\left(x\right)<0$ khi $x<-2\stackrel{}{\to }$$f\left(x\right)$  nghịch biến trên khoảng $\left(-\infty ;-2\right)$ .

Suy ra D đúng, B sai. Chọn B.