Cho hàm số y = (2m - 1)x + 2 - m có đồ thị là đường thẳng (d). a) Tìm m để hàm số đồng biến
Câu hỏi:
Cho hàm số y = (2m − 1)x + 2 − m có đồ thị là đường thẳng (d).
a) Tìm m để hàm số đồng biến? Hàm số nghịch biến?
b) Tìm m để (d) cắt Ox tại điểm có hoành độ bằng 3.
c) Tìm m để (d) song song với đường thẳng y = x + 3. Với giá trị của m vừa tìm được hãy vẽ đường thẳng (d); gọi giao điểm của (d) với Ox và Oy lần lượt là M, N. Tính diện tích tam giác OMN.
d) Cho các đường thẳng d1: 2x − y + 7 = 0; d2: x + y − 1 = 0. Tìm m để 3 đường thẳng d; d1; d2 đồng quy.
Trả lời:
a) Hàm số đồng biến khi \(2m - 1 > 0 \Leftrightarrow m > \frac{1}{2}\)
Hàm số nghịch biến khi \(2m - 1 < 0 \Leftrightarrow m < \frac{1}{2}\)
b) d đi qua điểm (3; 0) Û 0 = 3(2m − 1) + 2 − m
\( \Leftrightarrow m = \frac{1}{5}\)
c) \(d\;{\rm{//}}\;y = x + 3 \Leftrightarrow \left\{ \begin{array}{l}2m - 1 = 1\\2 - m \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\m \ne - 1\end{array} \right. \Leftrightarrow m = 1\)
Þ d: y = x + 1.
Ta có đồ thị hàm số:
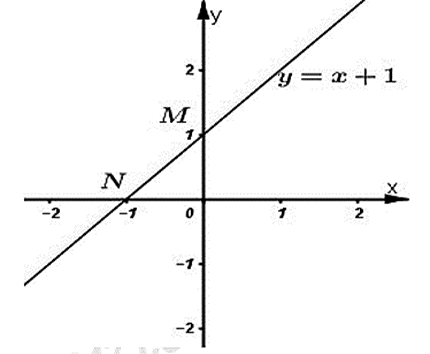
Ta có: OM = 1; ON = |−1| = 1
\( \Rightarrow {S_{OMN}} = \frac{1}{2}OM\,.\,ON = \frac{1}{2}\)
Vậy \({S_{OMN}} = \frac{1}{2}\).
d) Gọi I là giao điểm của d1; d2. Khi đó tọa độ điểm I là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}2x - y + 7 = 0\\x + y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = - 7\\x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 3\end{array} \right.\)
Suy ra I(−2; 3).
Mà I Î d Þ 3 = −2(2m − 1) + 2 − m
Û 3 = −4m + 2 + 2 − m
Û 5m = 1
\( \Leftrightarrow m = \frac{1}{5}\).
Vậy \(m = \frac{1}{5}\) là giá trị cần tìm.

