Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng
Câu hỏi:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (A'BC).
Trả lời:
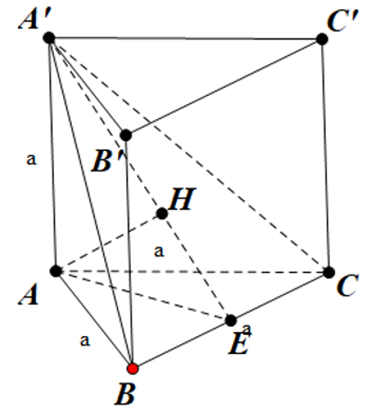
Gọi E là trung điểm của BC.
Ta có: \(\left\{ \begin{array}{l}A'E \bot BC\\AE \bot BC\end{array} \right. \Rightarrow \left( {A'AE} \right) \bot \left( {A'BC} \right)\)
Kẻ đường cao AH (H Î A'E) Þ AH ^ (A'BC)
Þ d(A, (A'BC)) = AH
\( = \sqrt {\frac{{A'{A^2}\,.\,A{E^2}}}{{A'{A^2} + A{E^2}}}} = \sqrt {\frac{{{a^2}\,.\,{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}} = \frac{{a\sqrt {21} }}{7}\).
Vậy khoảng cách từ A đến mặt phẳng (A'BC) bằng \(\frac{{a\sqrt {21} }}{7}\).

