Cho khối lăng trụ tam giác đều ABC.A'B'C'. Gọi M là trung điểm cạnh AA'. Mặt phẳng
Câu hỏi:
Cho khối lăng trụ tam giác đều ABC.A'B'C'. Gọi M là trung điểm cạnh AA'. Mặt phẳng (MBC) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
Trả lời:
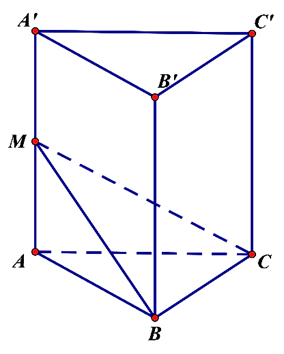
Mặt phẳng (MBC) chia khối lăng trụ thành hai phần M.ABC và MA'B'C'BC. Ta có:
\({V_{M.ABC}} = \frac{1}{3}\,.\,\frac{1}{2}h\,.\,{S_{ABC}} = \frac{1}{6}{V_{ABC.A'B'C'}}\)
Suy ra \({V_{MA'B'C'BC}} = \frac{5}{6}{V_{ABC.A'B'C'}}\)
Tỉ số thể tích cua hai phần đó bằng:
\(\frac{{{V_{M.ABC}}}}{{{V_{MA'B'C'BC}}}} = \frac{{\frac{1}{6}{V_{ABC.A'B'C'}}}}{{\frac{5}{6}{V_{ABC.A'B'C'}}}} = \frac{1}{5}\).

