Cho hàm số y = ax^2 + bx + c có đồ thị như hình bên. Khẳng định nào sau đây đúng? A. a > 0, b < 0, c < 0. B. a > 0, b < 0, c > 0. C. a > 0, b > 0, c > 0. D. a < 0, b < 0, c > 0.
Câu hỏi:
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
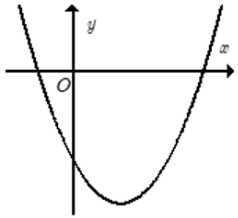
Khẳng định nào sau đây đúng?
A. a > 0, b < 0, c < 0.
B. a > 0, b < 0, c > 0.
C. a > 0, b > 0, c > 0.
D. a < 0, b < 0, c > 0.
Trả lời:
Lời giải
Đáp án đúng là: A
Bề lõm của đồ thị hướng lên nên a > 0.
Hoành độ đỉnh parabol \(x = \frac{{ - b}}{{2a}} > 0\).
Mà a > 0.
Suy ra –b > 0.
Do đó b < 0.
Parabol cắt trục tung tại điểm có tung độ âm nên c < 0.
Vậy a > 0, b < 0, c < 0.
Do đó ta chọn phương án A.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số f(x) = mx + m – 1. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = 0 có nghiệm thuộc (3; 4).
Xem lời giải »
Câu 2:
Tính diện tích hình thang ABCD, biết AB // CD, \(\widehat D = 90^\circ \), \(\widehat C = 38^\circ \), AB = 3,5 cm, AD = 3,1 cm.
Xem lời giải »
Câu 3:
Cho hình bình hành ABCD có AC vuông góc AD, AD = 3,5 cm, \(\widehat D = 60^\circ \). Tính diện tích hình bình hành ABCD.
Xem lời giải »
Câu 4:
Một cửa hàng giảm giá 10% so với giá bán bình thường nhưng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì lãi bao nhiêu phần trăm so với giá vốn?
Xem lời giải »
Câu 5:
Cho hàm số y = mx + 3. Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng d là lớn nhất.
Xem lời giải »
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và SA ⊥ (ABCD). Biết \(SA = AD = a\sqrt 2 \), AB = BC = a. Tính khoảng cách h từ C đến mặt phẳng (SBD).
Xem lời giải »


