Cho hàm số y = f(x) có đạo hàm trên R và f'(x) < 0, với mọi x thuộc (0; + vô cùng
Câu hỏi:
Cho hàm số y = f(x) có đạo hàm trên và . Biết . Khẳng định nào sau đây đúng
A.
B.
C.
D.
Trả lời:
Đáp án A
Do nên hàm số nghịch biến trên
Do đó
Áp dụng tính chất trên ta được:
+) , suy ra A đúng.
+ ) , suy ra B sai.
+) Do nên không đủ căn cứ để đưa ra kết luận , suy ra C sai.
+) , suy ra D sai.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong các hàm số sau, hàm số nào nghịch biến trên ?
Xem lời giải »
Câu 2:
Cho hàm số . Khẳng định nào dưới đây là SAI?
Xem lời giải »
Câu 5:
Cho hàm bậc ba có đồ thị đạo hàm như hình sau:
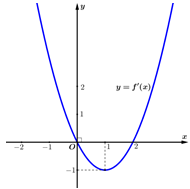
Hàm số đã cho nghịch biến trên khoảng
Xem lời giải »

