Cho hình chóp S .ABC có G là trọng tâm tam giác ABC. Gọi M là điểm trên cạnh
Câu hỏi:
Cho hình chóp S .ABC có G là trọng tâm tam giác ABC. Gọi M là điểm trên cạnh SA sao cho MA = 2MS, K là trung điểm BC và D là điểm đối xứng của G qua A.
a) Tìm giao điểm H của SK với (MCD).
b) Tính tỉ số \(\frac{{HK}}{{SK}}\).
Trả lời:
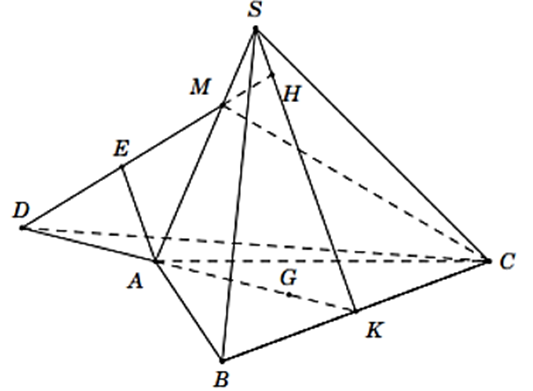
a) Trong mặt phẳng (SDK) kéo dài DM cắt SK tại H
Lúc đó H = SK ∩ (MCD)
b) Trong mặt phẳng (SDK) vẽ đường thẳng qua A song song với SK cắt DH tại E.
Vì AE // SH nên theo hệ quả của định lý Ta–lét ta có:
\(\frac{{AE}}{{SH}} = \frac{{MA}}{{MS}} = 2\). Suy ra: SH = \(\frac{1}{2}AE\)
Trong tam giác DHK có AE // HK nên ta có:
\(\frac{{AE}}{{HK}} = \frac{{DA}}{{DK}} = \frac{2}{5}\). Suy ra: \(HK = \frac{2}{5}AE\)
Ta có: SK = SH + HK = \(\frac{1}{2}AE + \frac{5}{2}AE = 3AE\)
Vậy \(\frac{{HK}}{{SK}} = \frac{{\frac{5}{2}AE}}{{3AE}} = \frac{5}{6}\).

