Cho hình chóp S.ABC có đáy ABC là ta giác vuông cân tại A, cạnh AB = 2a. Tam giác
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là ta giác vuông cân tại A, cạnh AB = 2a. Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy Gọi M là trung điểm của SB và N là điểm trên cạnh SC sao cho SC = 3SN. Tính thể tích V của khôi chóp S.AMN.
Trả lời:
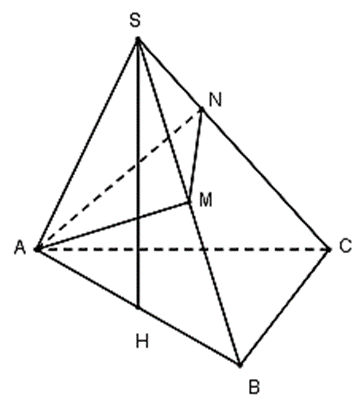
Gọi H là trung điểm của AB, vì tam giac SAB là tam giác đều nên SH ^ AB.
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right. \Rightarrow SH \bot \left( {ABC} \right)\)
Tam giác SAB đều cạnh 2a nên
\(SH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)
\({S_{ABC}} = \frac{1}{2}\,.\,2a\,.\,2a = 2{a^2}\)
\( \Rightarrow {V_{S.ABC}} = \frac{1}{2}SH\,.\,{S_{ABC}} = \frac{1}{3}\,.\,a\sqrt 3 \,.\,2{a^2} = \frac{{2{a^3}\sqrt 3 }}{3}\)
Lại có:
\(\frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}}\,.\,\frac{{SN}}{{SC}} = \frac{1}{2}\,.\,\frac{1}{3} = \frac{1}{6}\)
\( \Rightarrow {V_{S.AMN}} = \frac{1}{6}{V_{S.ABC}} = \frac{1}{6}\,.\,\frac{{2{a^3}\sqrt 3 }}{3} = \frac{{{a^3}\sqrt 3 }}{9}\).

