Cho hình chóp S.ABC có SA vuông góc (ABC). AB = a, Ac = a căn bậc hai 2
Câu hỏi:
Cho hình chóp S.ABC có SA ^ (ABC). AB = a; \(AC = a\sqrt 2 ;\;\widehat {BAC} = 45^\circ \). Gọi B1, C1 lần lượt là hình chiều vuông góc của A lên SB, SC. Tính thể tích mặt cầu ngoại tiếp hình chóp A.BCC1B1.
Trả lời:
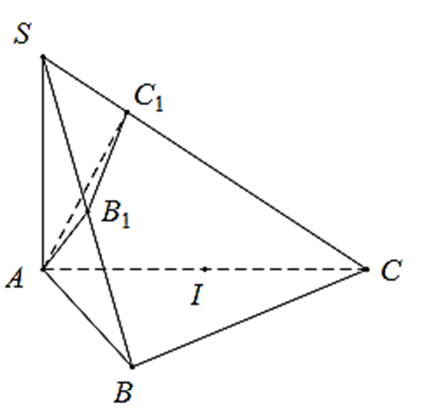
Tam giác ABC có AB = a; \(AC = a\sqrt 2 ;\;\widehat {BAC} = 45^\circ \) nên theo định lý cosin ta có:
BC2 = AB2 + AC2 − 2AB.AC.cos 45° = a2
Þ BC = a
Suy ra ∆ABC vuông cân tại B
Gọi I là trung điểm AC, ta có IA = IC = IB
Vì AC1 ^ SC nên IA = IC = IC1
Vì BC ^ SA, BC ^ AB
Þ BC ^ (SAB) Þ BC ^ AB1
Mà AB1 ^ SB Þ AB1 ^ (SBC)
Þ AB1 ^ B1C
Þ IA = IC = IB1
Vậy I là tâm mặt cầu ngoại tiếp chóp A.BCC1B1.
Bán kính của khối cầu đó là: \(R = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\).
Thể tích khối cầu đó là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 2 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 2 }}{3}\).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số f (x) đồng biến trên khoảng (a; b). Mệnh đề nào sau đây sai?
Xem lời giải »
Câu 2:
Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Tỉ số thể tích của khối chóp S.MNPQ và khối chóp S.ABCD bằng:
Xem lời giải »
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\).
Xem lời giải »
Câu 5:
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, cạnh bên SA vuông góc với đáy, M là trung điểm của BC, J là trung điểm của BM. Mệnh đề nào sau đây đúng?
Xem lời giải »
Câu 6:
Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?
Xem lời giải »
Câu 7:
Với tất cả các giá trị thực nào của tham số m thì hàm số y = x3 − 3(m + 1)x2 + 3m(m + 2)x nghịch biến trên đoạn [0; 1]?
Xem lời giải »
Câu 8:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 − 3(m + 2)x2 + 3(m2 + 4m)x + 1 nghịch biến trên khoảng (0; 1)?
Xem lời giải »


