Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA = \[a\sqrt 2 \], hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC.
Trả lời:
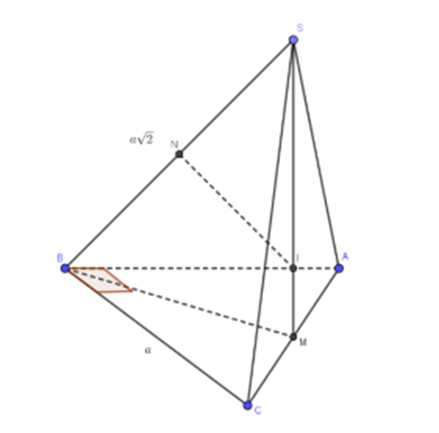
ΔABC vuông cân tại B có AB = a
\[ \Rightarrow AC = a\sqrt 2 \]
Gọi M là trung điểm AC
\[ \Rightarrow MA = MB = MC = \frac{1}{2}AC = a\sqrt 2 ;SM \bot (ABC)\]
Þ SM là trục của mặt phẳng đáy (ABC)
Gọi N là trung điểm SA
Trong mp(SAM) kẻ NI ⊥ SA (I ∈ SM)
Þ I là tâm mặt cầu ngoại tiếp khối chóp S.ABC
Ta có: ΔSNI ᔕ ΔSMA (g.g)
\[ \Rightarrow \frac{{SN}}{{SM}} = \frac{{SI}}{{SA}}\]
\[ \Rightarrow SI = R = \frac{{SA.SN}}{{SM}}\]
\[ \Rightarrow R = \frac{{S{A^2}}}{{2SM}} = \frac{{S{A^2}}}{{2\sqrt {S{A^2} - A{M^2}} }}\]
\[ \Rightarrow R = \frac{{a\sqrt 6 }}{3}\]
Vậy \[R = \frac{{a\sqrt 6 }}{3}\].
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Chứng minh trên đường tròn lượng giác gốc A, cung lượng giác \[\frac{{k2\pi }}{3}\] có các điểm biểu diễn tạo thành tam giác đều.
Xem lời giải »
Câu 2:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ dưới đây. Tìm số nghiệm của phương trình f(x) = 3.
Xem lời giải »
Câu 3:
Chứng minh hai góc kề nhau của một hình bình hành không thể có số đo là 40° và 50°.
Xem lời giải »
Câu 5:
Cho hình vuông ABCD có AB = 7cm. Tính độ dài các đoạn thẳng BC, DC, AD
Xem lời giải »
Câu 6:
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA′ và BB′. Tính thể tích của khối đa diện ABCIJC′.
Xem lời giải »
Câu 7:
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Tính thể tích khối chóp A.BCC’B’.
Xem lời giải »
Câu 8:
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Xem lời giải »



