Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B
Câu hỏi:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA = AC = 2a. Thể tích khối chóp S.ABC là
A. \({V_{S.ABC}} = \frac{2}{3}{a^3}\);
B. \({V_{S.ABC}} = \frac{{{a^3}}}{3}\);
C. VS.ABC = 2a3;
D. \({V_{S.ABC}} = \frac{{4{a^3}}}{3}\).
Trả lời:
Đáp án đúng là: A
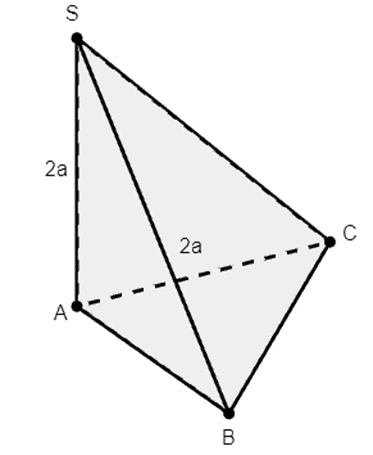
Do ∆ABC vuông cân tại B có:
AC = 2a
\( \Rightarrow AB = BC = \frac{{AC}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}\,.\,SA\,.\,\frac{1}{2}.\,BA\,.\,BC = \frac{1}{6}\,.\,2a\,.\,a\sqrt 2 \,.\,a\sqrt 2 = \frac{{2{a^3}}}{3}\).

