Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, cạnh AB = 3
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, cạnh AB = 3. Cạnh bên SA = 4 và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. \(\sqrt {34} \);
B. 6;
C. \(\frac{{\sqrt {34} }}{2}\);
D. \(2\sqrt 3 \).
Trả lời:
Đáp án đúng là: C
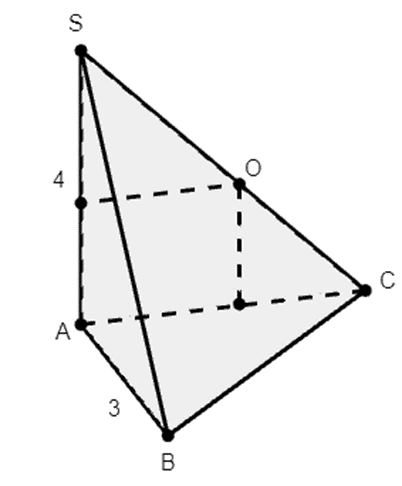
Gọi O là trung điểm của SC.
Khi đó O là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Ta có: AC2 = 32 + 32 = 18; SC2 = SA2 + AC2 = 42 + 18 = 34
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là: \(R = \frac{{SC}}{2} = \frac{{\sqrt {34} }}{2}\).

