Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a và SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 2 \). Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng BM và SC bằng
A. \(\frac{a}{2}\);
B. a;
C. \(\frac{{a\sqrt 2 }}{2}\);
D. \(a\sqrt 2 \).
Trả lời:
Đáp án đúng là: A
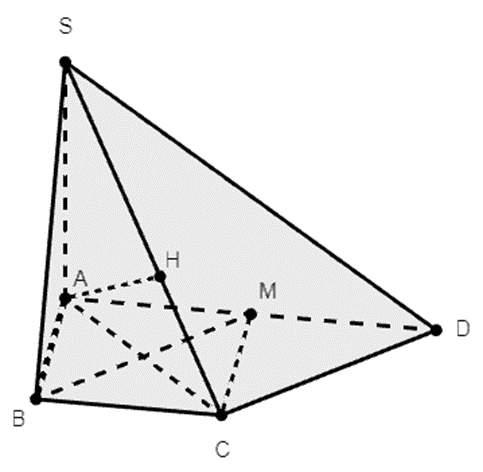
Xét tứ giác BMDC có: MD // BC và MD = BC = a
Do đó tứ giác BMDC là hình bình hành
Suy ra BM // CD nên BM // (SCD)
Khi đó d(BM, SC) = d(BM, (SCD)) = d(M, (SCD))
Mà d(M, (SCD) = \(\frac{1}{2}d\left( {A,(SCD)} \right)\)
Nên \(d(BM,SC) = \frac{1}{2}d(A,(SCD))\)
• Tứ giác AMCB là hình vuông nên cạnh AB = a nên \(AC = a\sqrt 2 \), CM = a
Do đó tam giác ACD có \(CM = \frac{1}{2}AD\) nên tam giác ACD vuông tại C hay AC ⊥ CD.
• Kẻ AH ⊥ SC tại H (1)
Ta có: \(\left\{ \begin{array}{l}CD \bot AC\\CD \bot SA\end{array} \right. \Rightarrow CD \bot (SAC) \Rightarrow (SCD) \bot (SAC)\) (2)
Từ (1) và (2) suy ra AH ⊥ (SCD) nên AH = d(A, (SCD))
Do \(SA = AC = a\sqrt 2 \) và SA⊥AC nên tam giác SAC vuông cân tại A.
⇒ H là trung điểm của SC
\( \Rightarrow AH = \frac{1}{2}SC = \frac{1}{2}\,.\,\sqrt 2 \,.\,SA = a\)
Vậy \(d(BM,SC) = \frac{a}{2}\).

