Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam
Câu hỏi:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Gọi H là hình chiếu của A trên SB. Tính khoảng cách giữa AH và BC.
Trả lời:
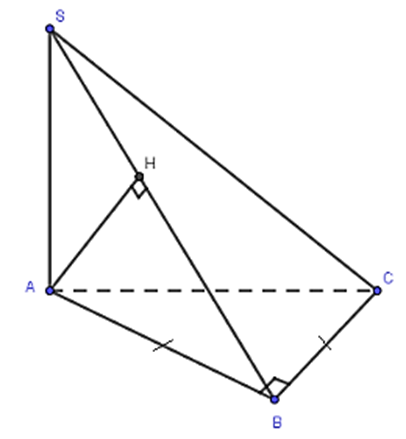
Ta có: BC ⊥ AB; BC ⊥ SA
Þ BC ⊥ (SAB) Þ BC ⊥ HB
Mà AH ⊥ HB Þ HB là đoạn vuông góc chung của AH và BC
Suy ra d(AH, BC) = HB
Tam giác SAB vuông cân tại A, có:
SA = AB = a
AH ⊥ SC
\[ \Rightarrow HB = \frac{1}{2}SB = \frac{1}{2}a\sqrt 2 = \frac{{a\sqrt 2 }}{2}\]
Vậy khoảng cách giữa AH và BC là \[\frac{{a\sqrt 2 }}{2}\].


