Cho hình chop S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác
Câu hỏi:
Cho hình chop S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và mặt phẳng đáy bằng 45°. Thể tích khối chóp S.ABCD bằng
A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\);
B. \(\frac{{{a^3}\sqrt 3 }}{9}\);
C. \(\frac{{{a^3}\sqrt 5 }}{{24}}\);
D. \(\frac{{{a^3}\sqrt 5 }}{6}\).
Trả lời:
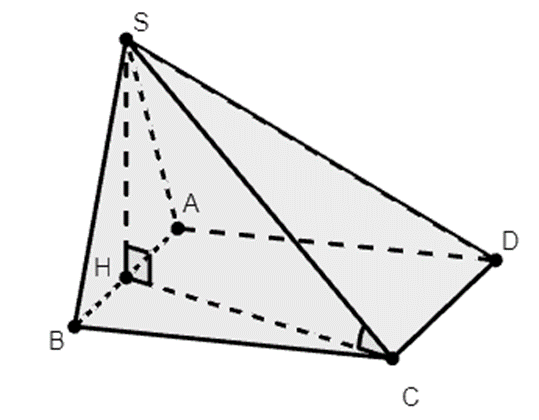
Đáp án đúng là: D
Gọi H là trung điểm của AB.
Vì ∆SAB cân tại S nên SH ⊥ AB
Ta có: (SAB) ⊥ (ABCD)
(SAB) ∩ (ABCD) = AB
SH ⸦ (SAB); SH ⊥ AB
⇒ SH ⊥ (ABCD)
\(\left( {\widehat {SC,(ABCD)}} \right) = \widehat {SCH} = 45^\circ \)
⇒ ∆SHC vuông cân tại H.
\( \Rightarrow SH = HC = \sqrt {B{C^2} + B{H^2}} = \sqrt {{a^2} + \frac{1}{4}{a^2}} = \frac{{a\sqrt 5 }}{2}\)
SABCD = AB2 = a2
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}\,.\,{S_{ABCD}}\,.\,SH = \frac{1}{3}\,.\,{a^2}\,.\,\frac{{a\sqrt 5 }}{2} = \frac{{{a^3}\sqrt 5 }}{6}\).