Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \(\frac{{{a^3}}}{6}\). Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
A. \(r = \frac{a}{{3 + \sqrt 3 }}.\)
B. r = 2a.
C. \(r = \frac{a}{{3\left( {3 + 2\sqrt 3 } \right)}}.\)
D. \(r = \frac{{2a}}{{3\left( {3 + 2\sqrt 3 } \right)}}.\)
Trả lời:
Đáp án đúng là: A
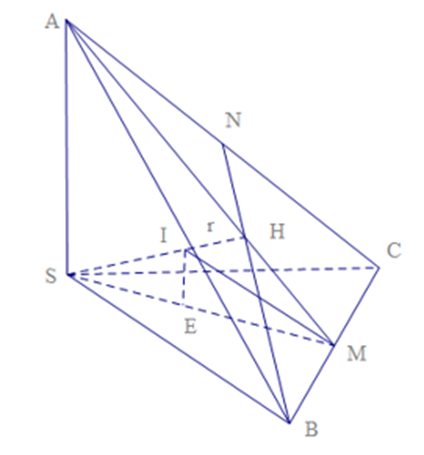
Áp dụng công thức: \(r = \frac{{3V}}{{{S_{tp}}}}\left( {\rm{*}} \right)\) và tam giác đều cạnh x có diện tích \(S = \frac{{{x^2}\sqrt 3 }}{4}\).
Từ giả thiết S.ABC dều có SA = SB = SC. Lại có SA, SB, SAC đôi một vuông góc và thể tích khối chóp \({\rm{S}}.{\rm{ABC}}\) bằng \(\frac{{{a^3}}}{6}\) nên ta có SA = SB = SC = a.
Suy ra \(AB = BC = CA = a\sqrt 2 \) và tam giác ABC đều cạnh có độ dài \(a\sqrt 2 \). Do đó diện tích toàn phần của khối chóp S.ABC là
Stp = SSAB + SSBC + SSCA + SABC
\( = 3\frac{{{a^2}}}{2} + \frac{{{{(a\sqrt 2 )}^2}\sqrt 3 }}{4} = \frac{{{a^2}\left( {3 + \sqrt 3 } \right)}}{2}\)
Thay vào \(\left( {\rm{*}} \right)\) ta được:
\(r = \frac{{3V}}{{{S_{tp}}}} = \frac{{3 \cdot \frac{{{a^3}}}{6}}}{{\frac{{{a^2}\left( {3 + \sqrt 3 } \right)}}{2}}} = \frac{a}{{3 + \sqrt 3 }}.\)

