Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng 60 độ. Biết rằng mặt

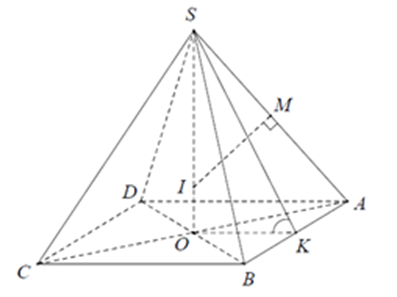
Gọi K là trung điểm của AB, O là giao điểm của AC và BD. Gọi M là trung điểm của SA

Góc giữa mặt bên và đáy là $\widehat {SKO} = 60^\circ$

Trong tam giác SOA dựng đường thẳng trung trực MI của SA, I ∈ SO

Suy ra I là tâm mặt cầu ngoại tiếp hình chóp tứ giác

Đặt AB = b

Vì ABCD là hình vuông cạnh b có hai đường chéo cắt nhau tại O

Suy ra $AK = BK = OK = \frac{1}{2}AB = \frac{b}{2}$ và tam giác OAK vuông tại K

Do đó $OA = \sqrt {O{K^2} + K{{\rm{A}}^2}} = \sqrt {{{\left( {\frac{b}{2}} \right)}^2} + {{\left( {\frac{b}{2}} \right)}^2}} = \frac{{b\sqrt 2 }}{2}$

Xét tam giác SOK có $\tan 60^\circ = \frac{{SO}}{{OK}} \Rightarrow SO = OK.\tan 60^\circ = \frac{{b\sqrt 3 }}{2}$

Vì tam giác SOA vuông tại O nên theo định lý Pytago có:

${\rm{S}}A = \sqrt {S{O^2} + O{A^2}} = \sqrt {{{\left( {\frac{{b\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{b\sqrt 2 }}{2}} \right)}^2}} = \frac{{b\sqrt 5 }}{2}$

Xét ∆SMI và ∆SOA có:

$\widehat {SMI} = \widehat {SOA}\left( { = 90^\circ } \right)$

Chung góc $\widehat {ASO}$

Do đó (g.g)

Suy ra $\frac{{SI}}{{SA}} = \frac{{SM}}{{SO}}$

Suy ra ${\rm{S}}I = \frac{{SM.SA}}{{SO}} = \frac{{\frac{1}{2}S{A^2}}}{{SO}} = \frac{{\frac{1}{2}.{{\left( {\frac{{b\sqrt 5 }}{2}} \right)}^2}}}{{\frac{{b\sqrt 3 }}{2}}} = \frac{{5\sqrt 3 b}}{{12}}$

Mà $\frac{{5\sqrt 3 b}}{{12}} = a\sqrt 3 \Rightarrow b = \frac{{12}}{5}a$

Vậy ta chọn đáp án A.