Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính cosin của góc
Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính cosin của góc giữa một mặt bên và một mặt đáy.
Trả lời:
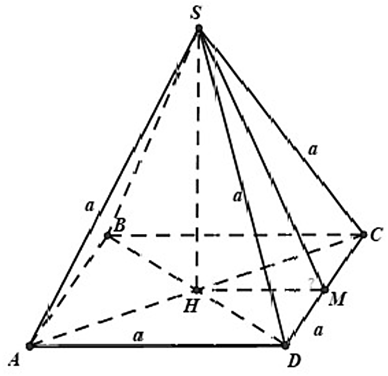
Gọi H là giao điểm của AC và BD.
Do S.ABCD là hình chóp tứ giác đều nên SH ^ (ABCD)
Ta có: (SCD) Ç (ABCD) = CD.
Gọi M là trung điểm của CD.
Tam giác SCD cân tại S có M là trung điểm của CD nên SM ^ CD
Tam giác CHD cân tại H (Theo tính chất đường chéo hình vuông) có M là trung điểm của CD nên HM ^ CD
Do đó \( \Rightarrow \left( {\widehat {\left( {SCD} \right);\;\left( {ABCD} \right)}} \right) = \left( {\widehat {SM;\;HM}} \right) = \widehat {SMH} = \alpha \)
Từ giả thiết suy ra tam giác SCD là tam giác đều cạnh a có SM là đường trung tuyến suy ra \(SM = \frac{{a\sqrt 3 }}{2}\).
Vậy \(\cos \alpha = \frac{{HM}}{{SM}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{1}{{\sqrt 3 }}\).

