Cho hình hộp ABCD.EFGH có vecto AB = vecto a, vecto AD = vecto b, vecto AE = vecto c
Câu hỏi:
Cho hình hộp ABCD.EFGH có \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b ,\overrightarrow {AE} = \overrightarrow c \). Gọi I là trung điểm của BG. Hãy biểu thị \(\overrightarrow {AI} \) theo \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \].
Trả lời:
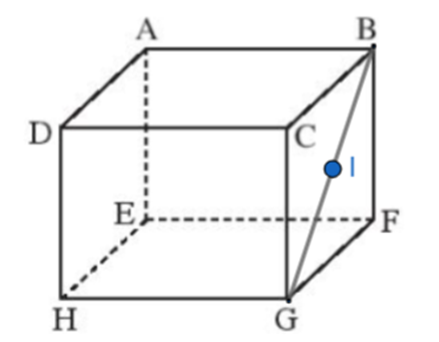
\(\overrightarrow {AI} = \overrightarrow {AB} + \overrightarrow {BI} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BG} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AH} \)
\[ = \overrightarrow {AB} + \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AE} } \right) = \overrightarrow a + \frac{1}{2}\overrightarrow b + \frac{1}{2}\overrightarrow c \].

