Cho tam giác ABC cân tại A và góc A = 36 độ. Chứng minh rằng: AB^2 = AB.BC
Câu hỏi:
Cho tam giác ABC cân tại A và \(\widehat A = 36^\circ \). Chứng minh rằng: AB2 = AB.BC + BC2.
Trả lời:
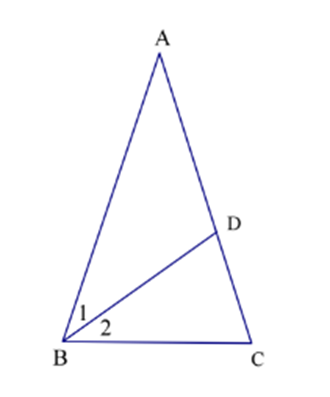
Kẻ phân giác BD của \(\widehat {ABC}\)(D thuộc AC).
Khi đó: \(\widehat {{B_1}} = \widehat {B2} = 36^\circ \)
Suy ra: tam giác ABD cân tại D và tam giác BCD cân tại B
Nên AD = BC = BD
Theo tính chất đường phân giác trong tam giác ABC có:
\(\frac{{BA}}{{BC}} = \frac{{AC}}{{CD}}\) ⇒ \(\frac{{BA}}{{BC}} = \frac{{BC}}{{AC - AD}}\)
Mà AB = AC; AD = BC
Nên \(\frac{{BA}}{{BC}} = \frac{{BC}}{{BA - BC}}\) ⇔ BA(BC – BC) = BC2
⇔ AB2 – BA.BC = BC2
⇔ AB2 = AB.BC + BC2

