Câu hỏi:
Cho tam giác ABC, đường phân giác AD. Chứng minh AD2 < AB.AC.
Trả lời:
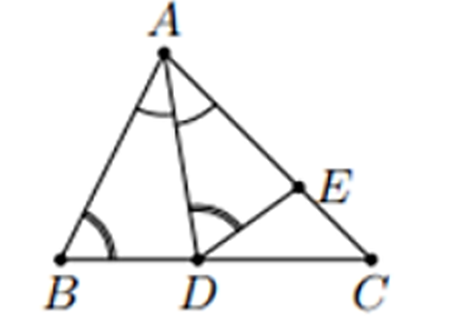
Lấy E trên AC sao cho \(\widehat {ADE} = \widehat B\)
Xét ∆ADE và ∆ABD có:
\(\widehat {ADE} = \widehat B\)
\(\widehat {BAD} = \widehat {DAE}\)
⇒ ∆ADE ∽ ∆ABD (g.g)
⇒ \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AD}}\) ⇒AD2 = AB.AE < AB.AC.
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–1; 2); B(3; 2); C(1; 5). Tính tọa độ trọng tâm của tam giác ABC?
Câu 2:
Trong mặt phẳng Oxy cho các điểm A(–1; 2); B(5; 8) điểm M thuộc Ox sao cho tam giác MAB vuông tại A. Tính diện tích tam giác MAB?
Câu 3:
Cho các số x, y, z dương thoả mãn x2 + y2 + z2 = 1. Tìm giá trị nhỏ nhất của biểu thức M = \(\frac{1}{{16{x^2}}} + \frac{1}{{4{y^2}}} + \frac{1}{{{z^2}}}\).
Câu 4:
Tìm số lớn nhất có 4 chữ số khác nhau, chữ số hàng trăm là chữ số 5. Số này phải chia hết cho 2 và chia hết cho 5.
Câu 5:
Cho tam giác ABC có trọng tâm G. H là điểm đối xứng với B qua G. Biểu diễn \(\overrightarrow {AH} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
Câu 6:
Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A; D; H; E cùng nằm trên một đường tròn (gọi tâm của nó là O).
b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến đường tròn (O).
Câu 7:
Cho tam giác ABC có BC = 10 cm, chiều cao AH = 9 cm.
a) Tính diện tích tam giác ABC.
b) Gọi M và N lần lượt là trung điểm của AB và AC. P và Q là trung điểm của AM, AN. Tính diện tích tam giác AMN.
Câu 8:
Cho đường tròn (O) đường kính AB, E thuộc đoạn AO (E khác A, O và AE > EO). Gọi H là trung điểm của AE , kẻ dây CD vuông góc với AE tại H.
a) Tính góc ACB ?
b) Tứ giác ACED là hình gì ?
c) Gọi I là giao điểm của DE và BC . Chứng minh HI là tiếp tuyến của đường tròn đường kính EB ?
