Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B
Câu hỏi:
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, \(\widehat {ACB} = 60^\circ \), cạnh BC = a, đường chéo A’B tạo với mặt phẳng (ABC) một góc 30°. Thể tích khối lăng trụ đứng ABC. A’B’C’ là:
A. \(\frac{{{a^3}\sqrt 3 }}{2}\)
B. \(\frac{{{a^3}\sqrt 3 }}{3}\)
C. \[{{\rm{a}}^3}\sqrt 3 \]
D. \(\frac{{3{a^3}\sqrt 3 }}{2}\).
Trả lời:
Đáp án đúng là: A
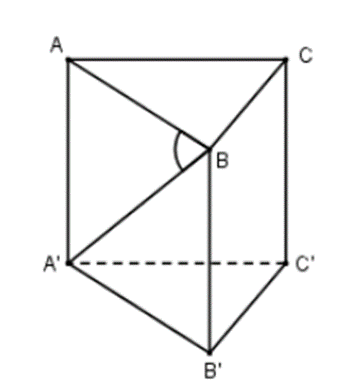
Vì \(AA' \bot (ABC)\) nên AB là hình chiếu vuông góc của A’B lên (ABC)
\(\widehat {\left( {A'B;\left( {ABC} \right)} \right)} = \left( {\widehat {A'B;AB}} \right) = \widehat {A'BA} = 30^\circ \)
Xét tam giác ABC vuông tại B có: \(AB = BC.\tan 60^\circ = a\sqrt 3 \)
Ta có AA’ ⊥ (ABC) ⊃ AB suy ra AA’ ⊥ AB
Do đó tam giác ABA’ vuông tại A
Suy ra \[{\rm{AA}}' = AB.\tan \widehat {A'BA} = a\sqrt 3 .\tan 30^\circ = a\sqrt 3 .\frac{1}{{\sqrt 3 }} = a\]
Diện tích tam giác ABC là \[{S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}a\sqrt 3 .a = \frac{{{a^2}\sqrt 3 }}{2}\]
Thể tích khối lăng trụ đứng ABC. A’B’C’ là: \(V = AA'.{S_{ABC}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)
Vậy đáp án cần chọn là A.

![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
