Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BA' và B'D' bằng bao nhiêu
Câu hỏi:
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BA' và B'D' bằng bao nhiêu?
Trả lời:
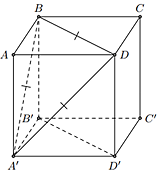
Do BD // B'D' nên góc giữa hai đường thẳng BA' và B'D' bằng góc giữa hai đường thẳng BA' và BD.
Do ABCD.A'B'C'D' là hình lập phương nên ∆A'BC là tam giác đều.
Khi đó
Vậy góc giữa hai đường thẳng BA' và B'D' bằng: 60°.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Đa thức P (x) = 32x5 − 80x4 + 80x3 − 40x2 + 10x − 1 là khai triển của nhị thức nào dưới đây?
Xem lời giải »
Câu 2:
Cho đoạn thẳng AB. Vị trí của điểm M thỏa mãn: được xác định bởi:
Xem lời giải »
Câu 3:
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Xem lời giải »
Câu 4:
Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng: .
Xem lời giải »
Câu 5:
Cho số phức z thỏa mãn |z + i + 1| = |z − 2i|. Tìm giá trị nhỏ nhất của modun của số phức z.
Xem lời giải »
Câu 6:
Cho số phức z thỏa mãn . Tìm giá trị nhỏ nhất của |z|.
Xem lời giải »
Câu 7:
Cho số phức z thỏa mãn |z − 4 − i| = |z + i|. Gọi z = a + bi (a; b Î ℝ) là số phức thỏa mãn |z − 1 + 3i| nhỏ nhất. Giá trị của biểu thức T = 2a + 3b là:
Xem lời giải »
Câu 8:
Cho các số phức z thỏa mãn |z − 2i| = |z + 2|. Gọi z là số phức thỏa mãn |(2 − i)z + 5| nhỏ nhất. Khi đó:
Xem lời giải »


