Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy
Câu hỏi:
Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng (SAB) bằng \(\frac{{a\sqrt 3 }}{3}\), \(\widehat {SAO}\) = 30°, \(\widehat {SAB}\) = 60°. Độ dài đường sinh của hình nón theo a bằng?
Trả lời:
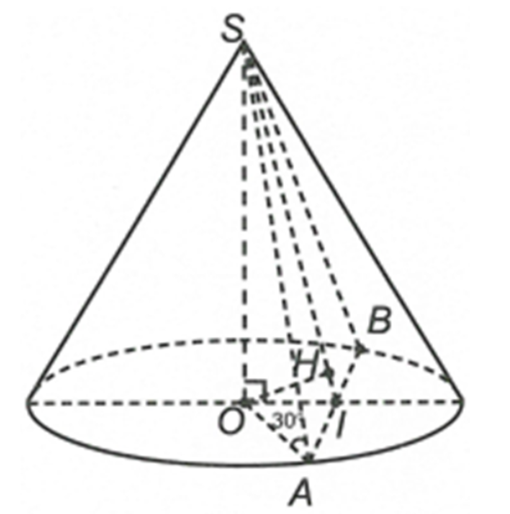
Gọi I là trung điểm AB, dựng OH vuông góc SI
Ta có: OH = \(\frac{{a\sqrt 3 }}{3}\)
Do \(\widehat {SAB}\)= 60° nên tam giác SAB đều.
Suy ra: SA = SB = AB
Mặt khác \(\widehat {SAO}\) = 30° nên SO = SA. sin30° = \(\frac{1}{2}\)SA
Và OA = SA. cos 30° = \(\frac{{SA\sqrt 3 }}{2}\)
Xét tam giác SOI ta có:
\[\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{A^2} - A{I^2}}} = \frac{1}{{{{\left( {\frac{{SA}}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{SA\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{{SA}}{2}} \right)}^2}}}\]
⇒ \[\frac{1}{{O{H^2}}} = \frac{6}{{S{A^2}}}\]⇒ SA = \(OH\sqrt 6 = \frac{{a\sqrt 3 }}{3}.\sqrt 6 = a\sqrt 2 \)

