Cho tam giác ABC có AB = 2, BC = 3, AC = 4. M là trung điểm của BC, đường

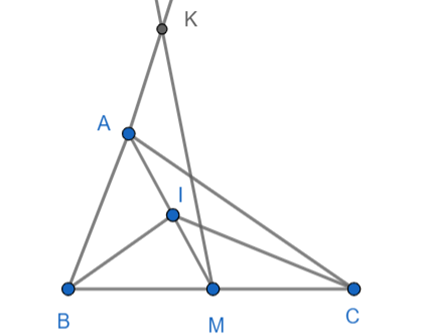
Đặt \(\overrightarrow {KA} = x\overrightarrow {AB} \)

Ta có: \(\frac{{AI}}{{IM}} = \frac{{AC}}{{MC}} = \frac{4}{{1,5}} = \frac{8}{3}\)⇒ \(\frac{{AI}}{{AM}} = \frac{8}{{11}}\)

\[\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} \]

⇒ \[\overrightarrow {AI} = \frac{8}{{11}}\overrightarrow {AM} = \frac{8}{{11}}\overrightarrow {AB} + \frac{4}{{11}}\overrightarrow {BC} \]

\(\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} = \frac{{ - 3}}{{11}}\overrightarrow {AB} + \frac{4}{{11}}\overrightarrow {BC} \)

\(\overrightarrow {KM} = \overrightarrow {KA} + \overrightarrow {AM} = x\overrightarrow {AB} + \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \left( {1 + x} \right)\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} \)

Vì KM vuông góc với BI nên \(\overrightarrow {BI} .\overrightarrow {KM} = 0\)

Hay \(\left( {\frac{{ - 3}}{{11}}\overrightarrow {AB} + \frac{4}{{11}}\overrightarrow {BC} } \right)\left[ {\left( {1 + x} \right)\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} } \right] = 0\)

Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b \)

Ta có: \(\frac{{ - 3\left( {1 + x} \right)}}{{11}}{\overrightarrow a ^2} + \frac{3}{{22}}\overrightarrow a .\overrightarrow b - \frac{{4\left( {1 + x} \right)}}{{11}}\overrightarrow a .\overrightarrow b + \frac{2}{{11}}{\overrightarrow b ^2} = 0\)

⇔ \(\frac{{ - 3\left( {1 + x} \right)}}{{11}}{.2^2} + \left( {\frac{{ - 4\left( {1 + x} \right)}}{{11}} + \frac{3}{{22}}} \right).\overrightarrow a .\overrightarrow b + \frac{2}{{11}}{.3^2} = 0\)

Lại có: \(\overrightarrow a .\overrightarrow b = 2.3.\frac{{{2^2} + {3^2} - {4^2}}}{{2.2.3}} = \frac{{ - 3}}{2}\)

⇒ \(\frac{{ - 12 - 12x}}{{11}} + \left( {\frac{{3 - 8 - 8x}}{{22}}} \right).\frac{{ - 3}}{2} + \frac{{18}}{{11}} = 0\)

⇔ x = \(\frac{{13}}{8}\)

Vậy \(\frac{{AK}}{{AB}}\)= \(\frac{{13}}{8}\).