Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng qua đỉnh của hình nón

Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông có diện tích bằng 4. Góc giữa đường cao của hình nón và mặt phẳng thiết diện bằng 30°. Tính thể tích của khối nón được giới hạn bởi hình nón đã cho.

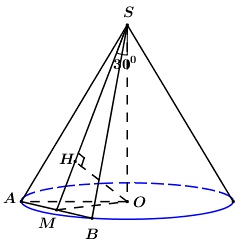
Giả sử mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông SAB.

Gọi M là trung điểm của AB Þ OM ^ AB (quan hệ vuông góc giữa đường kính và dây cung).

Trong (SOM) kẻ OH ^ SM (H Î SM) ta có:

$\left\{\begin{array}{l}AB\perp OM\\ AB\perp SO\end{array}\right.\Rightarrow AB\perp \left(SOM\right)\Rightarrow AB\perp OH$

$\left\{\begin{array}{l}OH\perp AB\\ OH\perp SM\end{array}\right.\Rightarrow OH\perp \left(SAB\right)$

Suy ra SH là hình chiếu của SO lên (SAB).

$\left(\widehat{SO;\left(SAB\right)}\right)=\left(\widehat{SO;SH}\right)=\widehat{HSO}=\widehat{MSO}=30°$

Theo bài ra ta có:

$S_{△SAB}=4\iff \frac{1}{2}SA.SB=4$

 $\iff S{A}^2=8\iff SA=2\sqrt{2}$

Tam giác SAB vuông cân tại S

 $\Rightarrow AB=SA\sqrt{2}=2\sqrt{2}.\sqrt{2}=4$

 $\Rightarrow SM=\frac{1}{2}AB=2$

Xét tam giác vuông SOM có:

$\left\{\begin{array}{l}SO=SM.\cos 30°=2.\frac{\sqrt{3}}{2}=\sqrt{3}=h\\ OM=SM.\sin 30°=2.\frac{1}{2}=1\end{array}\right.$

Áp dụng định lí Py-ta-go trong tam giác vuông OAM có:

 $OA=\sqrt{O{M}^2+A{M}^2}=\sqrt{1^2+2^2}=\sqrt{5}=R$

Vậy thể tích khối nón là:

 $V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi .{\left(\sqrt{5}\right)}^2.\sqrt{3}=\frac{5\pi \sqrt{3}}{3}$.