Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc
Câu hỏi:
Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc 45°. Tính thể tích của khối chóp S.ABC theo a.
Trả lời:
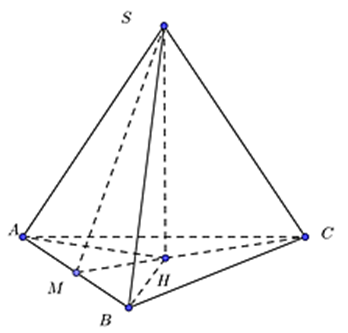
Gọi H là trọng tâm đáy trùng với hình chiếu của S, M là trung điểm của AB
Đặt \(AB = 6x \Rightarrow CM = 6x \cdot \frac{{\sqrt 3 }}{2} = 3x\sqrt 3 \)
\( \Rightarrow MH = x\sqrt 3 ;AH = HC = 2x\sqrt 3 \)
Góc tạo bởi mặt bên và mặt đáy là \(\widehat {SMH} = 45^\circ \Rightarrow SH = MH = x\sqrt 3 \)
Tam giác vuông SAH có: \({\rm{A}}{{\rm{H}}^2} + {\rm{S}}{{\rm{H}}^2} = {\rm{S}}{{\rm{A}}^2}\) (định lý Pytago)
\( \Leftrightarrow 12{x^2} + 3{x^2} = {a^2} \Leftrightarrow 15{{\rm{x}}^2} = {a^2}\)
\( \Rightarrow x = \frac{a}{{\sqrt {15} }}\)
Khi đó: \(V = \frac{1}{3}SH \cdot \frac{{A{B^2}\sqrt 3 }}{4} = \frac{1}{3} \cdot x\sqrt 3 \cdot \frac{{{{(6x)}^2}\sqrt 3 }}{4} = 9{x^3} = 9 \cdot {\left( {\frac{a}{{\sqrt {15} }}} \right)^3} = \frac{{{a^3}\sqrt {15} }}{{25}}\)
Vậy thể tích của khối chóp S.ABC là \(V = \frac{{{a^3}\sqrt {15} }}{{25}}\).


