Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng 60 độ, SA = 1, SB = 2, SC = 3
Câu hỏi:
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng 60°, SA = 1, SB = 2, SC = 3. Thể tích của khối chóp S.ABC bằng:
A. \(\frac{{\sqrt 2 }}{{72}}\)
B. \(\frac{{\sqrt 6 }}{2}\)
C. \(\frac{{\sqrt 2 }}{2}\)
D. \(\frac{{\sqrt 3 }}{2}\).
Trả lời:
Đáp án đúng là: C
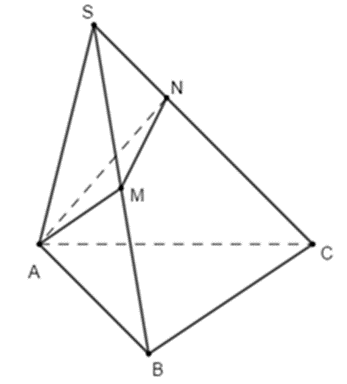
Ta lấy lần lượt trên cạnh SB, SC các điểm M, N sao cho \({\rm{SA}} = {\rm{SM}} = {\rm{SN}} = 1\)
Khi đó: \(\frac{{{{\rm{V}}_{{\rm{S}}.{\rm{ANM}}}}}}{{{{\rm{V}}_{{\rm{S}}.{\rm{ABC}}}}}} = \frac{{{\rm{SM}}}}{{{\rm{SB}}}} \cdot \frac{{{\rm{SN}}}}{{{\rm{AC}}}} = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}\)
Tứ diện SAMN có góc ở đỉnh S là 60° và các cạnh bên bằng 1
Suy ra SAMN là tứ diện đều. Áp dụng công thức tính thể tích tứ diện đều là \({\rm{V}} = \frac{{\sqrt 2 }}{{12}}{{\rm{a}}^3} = \frac{{\sqrt 2 }}{{12}}\)
Khi đó \({{\rm{V}}_{{\rm{SABC}}}} = 6.{V_{S.AMN}} = 6.\frac{{\sqrt 2 }}{{12}} = \frac{{\sqrt 2 }}{2}\)
Vậy đáp án cần chọn là C.

