Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60 độ
Câu hỏi:
Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60°. Thể tích của khối chóp đó bằng:
A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 3 }}{6}\)
C. \(\frac{{{a^3}\sqrt 3 }}{{36}}\)
D. \(\frac{{{a^3}\sqrt 3 }}{4}\).
Trả lời:
Đáp án đúng là: A
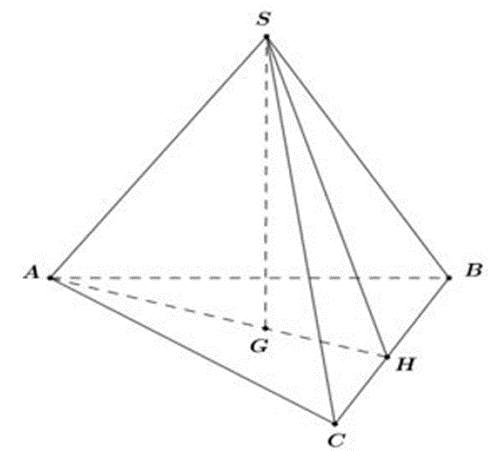
Gọi H là trung điểm BC và G là trọng tâm tam giác ABC
Ta có \(SG \bot (ABC)\). Tam giác ABC đều cạnh a nên và
\(AG = \frac{2}{3}AH = \frac{2}{3} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}.(SA\widehat {,(ABC)}) = \widehat {SAG} = 60^\circ \)
Trong tam giác vuông SGA ta có \(SG = AG \cdot \tan \widehat {SAG} = \frac{{a\sqrt 3 }}{3} \cdot \sqrt 3 = a\).
Vậy .

