Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, BD = 2a, góc giữa

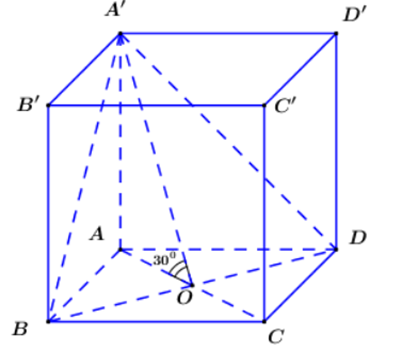
Ta có:

(A’BC) ∩ (ABCD) = BD

\(\left\{ \begin{array}{l}AA' \bot B{\rm{D}}\\AO \bot B{\rm{D}}\end{array} \right. \Rightarrow \left( {A'AO} \right) \bot B{\rm{D}}\)

\(\left\{ \begin{array}{l}\left( {A'AO} \right) \cap \left( {A'B{\rm{D}}} \right) = A'O\\\left( {A'AO} \right) \cap \left( {ABC{\rm{D}}} \right) = AO\end{array} \right.\)

Suy ra: \(\widehat {\left( {\left( {A'B{\rm{D}}} \right);\left( {ABC{\rm{D}}} \right)} \right)} = \widehat {\left( {A'O,AO} \right)} = \widehat {AO{\rm{A}}'} = 30^\circ \)

Vì ABCD là hình vuông có hai đường chéo cắt nhau tại O

Suy ra O là trung điểm của AC và BD

Do đó \(AO = \frac{1}{2}AC = \frac{1}{2}B{\rm{D}} = a\)

Xét tam giác A’OA vuông tại A có \(AA' = \tan 30^\circ .AO = \frac{{a\sqrt 3 }}{3}\)

\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABC{\rm{D}}}}{\rm{.AA}}' = \frac{1}{2}AC.B{\rm{D}}.AA' = \frac{1}{2}.{(2a)^2} \cdot \frac{{a\sqrt 3 }}{3} = \frac{{2\sqrt 3 {a^3}}}{3}\)

Vậy ta chọn đáp án D.