Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ c đến BB′ là  căn 5, khoảng cách từ  A đến BB’ và CC′ lần lượt là 1; 2. Hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’

Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ c đến BB′ là  $\sqrt{5}$, khoảng cách từ  A đến BB’ và CC′ lần lượt là 1; 2. Hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’,  $A\text{'}M=\frac{\sqrt{15}}{3}$. Tính thể tích của khối lăng trụ đã cho.

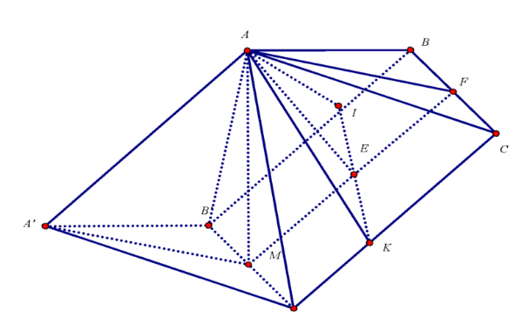
Kẻ  AI ⊥ BB′, AK ⊥CC′ (hình vẽ).

Khoảng cách từ A đến BB′ và CC′ lần lượt là 1; 2

Þ AI = 1, AK = 2

Gọi F là trung điểm của BC.

Ta có:  $AF=A\text{'}M=\frac{\sqrt{15}}{3}$

AI ⊥ BB′, BB’ ⊥ AK Þ BB’ ⊥ (AIK)

Hay BB’ ⊥ IK

Vì CC′ // BB′ ⇒ d(C, BB′) = d(K, BB′) = IK =  $\sqrt{5}$

Þ ΔAIK vuông tại A.

Gọi E là trung điểm của IK 

Þ EF // BB’ 

Þ EF ⊥ (AIK)

Þ EF ⊥ AE

Lại có: AM ⊥ (ABC)

Do đó góc giữa hai mặt phẳng (ABC) và (AIK) là góc giữa EF và AM 

 $\widehat{AME}=\widehat{FAE}$

$\cos \widehat{FAE}=\frac{AE}{AF}=\frac{\frac{\sqrt{5}}{2}}{\frac{\sqrt{15}}{3}}=\frac{\sqrt{3}}{2}$

 $\Rightarrow \widehat{FAE}=30°$

Hình chiếu vuông góc của tam giác ABC lên mặt phẳng (AIK) là ΔAIK nên ta có:

$S_{AIK}=S_{ABC}\cos \widehat{EAF}$

 $\Rightarrow S_{ABC}=\frac{2}{\sqrt{3}}$

Xét ΔAMF vuông tại A:  $\tan \widehat{AMF}=\frac{AF}{AM}$

 $\Rightarrow AM=\frac{\frac{\sqrt{15}}{3}}{\frac{\sqrt{3}}{3}}=\sqrt{5}\Rightarrow V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\sqrt{5}.\frac{2}{\sqrt{3}}=\frac{2\sqrt{15}}{3}$

Vậy $V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{2\sqrt{15}}{3}$.