Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố địn
Câu hỏi:
Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định.
Trả lời:
Lời giải
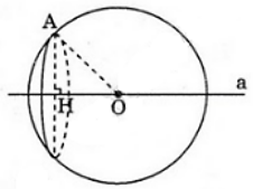
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hệ bất phương trình sau, biểu diễn hình học tập nghiệm:
\[\left\{ \begin{array}{l}2x - y \le 3\\2x + 5y \le 12x + 8\end{array} \right.\]
Xem lời giải »
Câu 2:
Biểu diễn miền nghiệm của của bất phương trình hai ẩn 2x − y ≥ 0.
Xem lời giải »
Câu 3:
Cho phương trình 5sin 2x + sin x + cos x + 6 = 0. Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?
Xem lời giải »
Câu 4:
Chứng minh phương trình sau đây vô nghiệm:
5sin 2x + sin x + cos x + 6 = 0.
Xem lời giải »
Câu 5:
Cho hàm số f (x) có đạo hàm trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề nào sai?
Xem lời giải »
Câu 6:
Cho hàm số y = f (x) có đạo hàm trên (a; b). Phát biểu nào sau đây sai?
Xem lời giải »
Câu 7:
Cho hàm số \(y = \frac{x}{2} + \cos x\). Mệnh đề nào sau đây đúng?
Xem lời giải »


