Cho nửa đường tròn (O), đường kính AB. Kẻ 2 tiếp tuyến Ax, By (Ax, By và nửa đường tròn
Câu hỏi:
Cho nửa đường tròn (O), đường kính AB. Kẻ 2 tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi C là một điểm thuộc tia Ax, kẻ tiếp tuyến CM với nửa đường tròn (M là tiếp điểm). CM cắt By tại D. Gọi I là giao điểm của OC và AM, K là giao điểm của OD và MB.
a) Tính \(\widehat {COD}.\)
b) Tứ giác OIMK là hình gì?
c) Chứng minh AC.BD không đổi khi C di chuyển trên Ax.
d) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Trả lời:
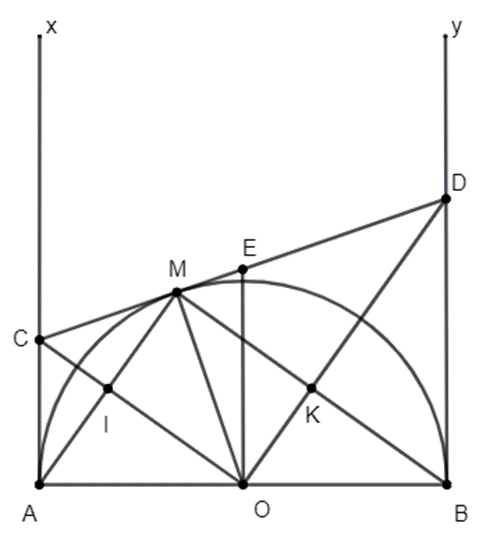
a) Vì AC và CM là tiếp tuyến cắt nhau tại C của (O) nên CO là tia phân giác của góc AOM.
Tương tự OD là tia phân giác của góc BOM.
Mà \(\widehat {MOA} + \widehat {MOB} = 180^\circ \) ⇒ OC ⊥ OD ⇒ \(\widehat {COD} = 90^\circ \)
b) Vì CM, CA là tiếp tuyến của (O) nên OI ⊥ AM hay \(\widehat {OAM} = 90^\circ \)
Tương tự OD ⊥ MB suy ra \(\widehat {OKM} = 90^\circ \)
Mà AB là đường kính của (O) nên AM ⊥ BM hay \(\widehat {IMK} = 90^\circ \)
Ta có: \(\widehat {OAM} = \widehat {OKM} = \widehat {IMK} = 90^\circ \)
Do đó tứ giác OIMK là hình chữ nhật.
c) Ta có CM, CA là tiếp tuyến của (O) nên CA = CM
Tương tự DM = DB.
Mà OC ⊥ OD, OM ⊥ CD suy ra MC.MD = OM2 = R2 hay AC.BD = R2
⇒ AC.BD không đổi khi C di chuyển trên Ax.
d) Gọi E là trung điểm của CD.
⇒ OE là đường trung bình của hình thang ABDC.
⇒ EO // AC ⇒ EO ⊥ AB
Mà ∆COD vuông tại O (do \(\widehat {COD} = 90^\circ \))
⇒ (E, EO) là đường tròn đường kính CD
⇒ AB là tiếp tuyến của đường tròn đường kính CD vì EO ⊥ AB

