Cho parabol (P): y = x^2 và đường thẳng (d): y = -x + 2. a) Vẽ (d) và (P) trên cùng một
Câu hỏi:
Cho parabol (P): y = x2 và đường thẳng (d): y = −x + 2.
a) Vẽ (d) và (P) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của parabol (P) và đường thẳng (d) bằng phép tính.
Trả lời:
a) Ta có:
(P) đi qua các điểm có tọa độ như bảng sau:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Đỉnh của (P) là O(0;0)
(d) đi qua các điểm có tọa độ (0;2), (2;0)
Ta có đồ thị như sau:
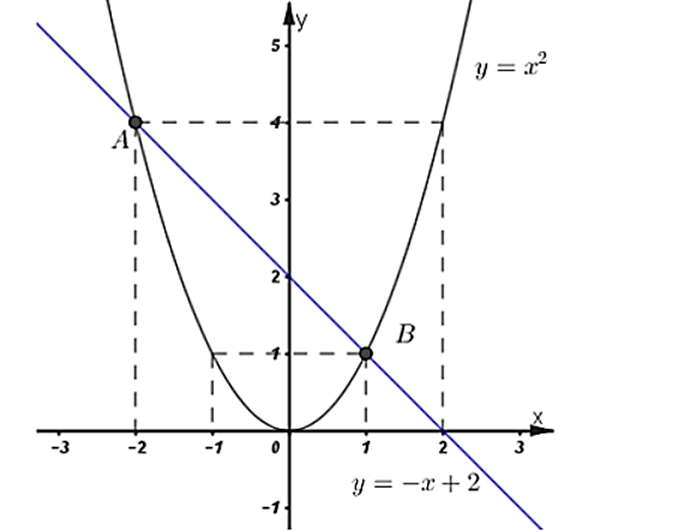
b) Xét phương trình hoành độ giao điểm:
x2 = –x + 2
⇔ x2 + x – 2 = 0
⇔ x2 + 2x – x – 2 = 0
⇔ x(x + 2) – (x + 2) = 0
⇔ (x + 2)(x – 1) = 0
⇔ \(\left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\)
⇒ \(\left[ \begin{array}{l}y = 4\\y = 1\end{array} \right.\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt A(−2; 4) và B(1; 1).

