Cho tam giác ABC cân tại A, trung tuyến BD, CK. Lấy điểm E sao cho C là trung điểm
Câu hỏi:
Cho tam giác ABC cân tại A, trung tuyến BD, CK. Lấy điểm E sao cho C là trung điểm của AE. Chứng minh BE = 2BD.
Trả lời:
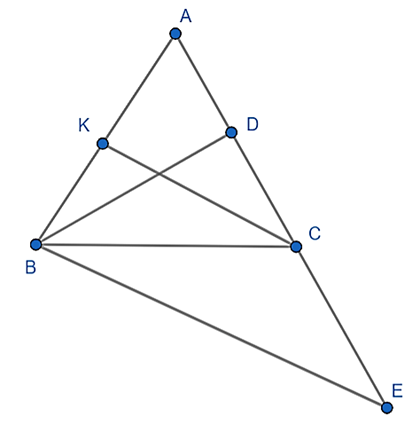
Xét tam giác ABE có K, C lần lượt là trung điểm AB, AC
Suy ra: KC là đường trung bình tam giác ABE
Nên: KC // BE và \(KC = \frac{1}{2}BE\) (1)
Xét tam giác ABD và tam giác ACK có:
AB = AC
Chung \(\widehat A\)
AD = AK (Vì AB = AC nên \(\frac{1}{2}AC = \frac{1}{2}AB\))
⇒ ∆ABD = ∆ACK (c.g.c)
⇒ BD = CK (2)
Từ (1) và (2) suy ra: BD = \(\frac{1}{2}BE\) hay BE = 2BD.

