Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H. a) Chứng minh rằng
Câu hỏi:
Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A; D; H; E cùng nằm trên một đường tròn (gọi tâm của nó là O).
b) Gọi M là trung điểm của BC. Chứng minh ME là tiếp tuyến đường tròn (O).
Trả lời:
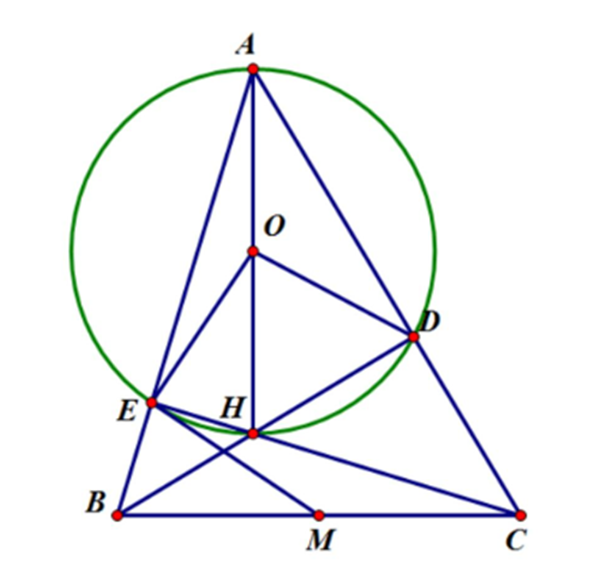
a. Gọi O là trung điểm AH
Xét tam giác AEH vuông tại H: O là trung điểm AH
⇒ AO = OH = OE Chứng minh tương tự ⇒ AO = OH = OD
⇒ OA = OH = OD = OE
Vậy A, D, H, E ∈ (O) với O là trung điểm AH
b. Có: BD giao CE = H ⇒ H là trực tâm tam giác ABC
⇒ AH ⊥ BC
Mà: CE ⊥ AB
⇒ \(\widehat {EAH} = \widehat {ECB}\) (1) (hai góc có cạnh tương ứng vuông góc)
Có: OA = OE⇒ tam giác AOE cân tại O
⇒ \(\widehat {AEO} = \widehat {EAO}\)(2)
Chứng minh tương tự ⇒ tam giác EMC cân tại M
⇒ \(\widehat {ECM} = \widehat {CEM}\)(3)
(1); (2); (3) ⇒ \(\widehat {AEO} = \widehat {CEM}\)
Mà: \(\widehat {AEO} + \widehat {OEC} = \widehat {AEC} = 90^\circ \)
⇒ \(\widehat {OEC} + \widehat {CEM} = \widehat {OEM} = 90^\circ \)
⇒ EM là tiếp tuyển của (O).

