Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tích vô hướng của hai vectơ
Câu hỏi:
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tích vô hướng của hai vectơ \(\overrightarrow {BC} .\overrightarrow {CG} \)
Trả lời:
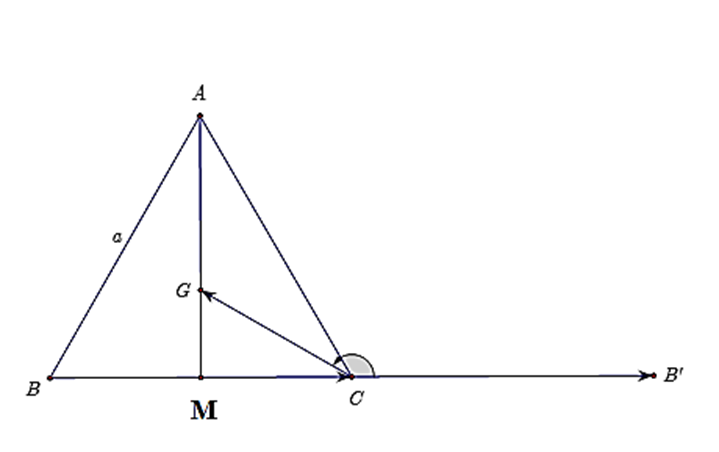
Gọi M là trung điểm BC
\(\tan \widehat {GCM} = \frac{{GM}}{{MC}} = \frac{{\frac{1}{3}AM}}{{\frac{1}{2}BC}} = \frac{{\frac{1}{3}.\frac{{a\sqrt 3 }}{2}}}{{\frac{1}{2}a}} = \frac{{\sqrt 3 }}{3}\)
Suy ra: \(\widehat {GCM} = 30^\circ \)
Suy ra: \(\widehat {GCB'} = 180^\circ - 30^\circ = 150^\circ \)
Lại có: GC = \(\sqrt {G{M^2} + M{C^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{6}} \right)}^2} + \frac{1}{4}{a^2}} = \frac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {BC} .\overrightarrow {CG} = BC.CG.\cos \left( {\widehat {\overrightarrow {BC} ,\overrightarrow {CG} }} \right) = BC.CG.\cos \left( {\widehat {\overrightarrow {CB'} ,\overrightarrow {CG} }} \right) = BC.CG.\cos \widehat {GCB'}\)
\( = a.\frac{{a\sqrt 3 }}{3}.\cos 150^\circ = - \frac{{{a^2}}}{2}\).

