Cho tam giác ABC đều có cạnh bằng a. Diện tích tứ giác BCDE là
Câu hỏi:
Cho tam giác ABC đều có cạnh bằng a. Diện tích tứ giác BCDE là?
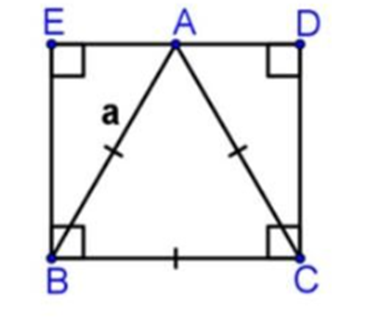
Trả lời:
△ABC đều ⇒ \(\widehat {ABC} = 60^\circ \)
⇒ \(\widehat {ABE} = 90^\circ - 60^\circ = 30^\circ \)
⇒ \(AE = \frac{1}{2}AB = \frac{a}{2}\) (trong tam giác vuông, cạnh đối diện với góc 30 độ bằng \(\frac{1}{2}\) cạnh huyền)
Áp dụng định lý Pytago vào △ABE ta có:
AB2 = AE2 + BE2
Suy ra: BE = \(\sqrt {A{B^2} - A{E^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
SBDCE = BE.BC = \(\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^2}\sqrt 3 }}{2}\).

