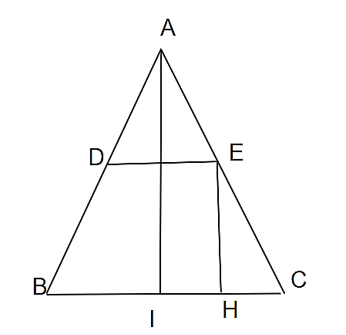
Cho tam giác ABC. Gọi D, E theo thứ tự là trung điểm AB, AC. Chứng minh: a) Xác định dạng tứ giác BDEC.
Câu hỏi:
Cho tam giác ABC. Gọi D, E theo thứ tự là trung điểm AB, AC. Chứng minh:
a) Xác định dạng tứ giác BDEC.
Trả lời:
a)
Ta có: AB = AC
D là trung điểm AB và E là trung điểm AC nên DB = EC = (1)
Lại có: DE là đường trung bình của tam giác ABC nên DE // BC (2)
Từ (1) và (2) suy ra: DECB là hình thang cân.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Để lát một căn phòng hình chữ nhật có chiều dài 12m, chiều rộng 8m, người ta dùn gạch men hình vuông có cạnh 4 dm. Hỏi cần bao nhiêu viên gạch để lát kín căn phòng đó?
Xem lời giải »
Câu 2:
Tìm x biết x chia hết cho 15 và 12; biết 0 < x < 150.
Xem lời giải »
Câu 3:
Tìm số tự nhiên x biết: 70 ⋮ x, 84 ⋮ x và x > 8.
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh AEHF là hình chữ nhật.
Xem lời giải »
Câu 5:
b) Kẻ DK vuông góc BC, EH vuông góc BC và BC = 8 cm. Tính HC và HB.
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông tại A. Đường cao AH, qua H kẻ HM vuông góc với AB, HD vuông góc với AC. Gọi E là trung điểm BC. Chứng minh AE vuông góc với DM.
Xem lời giải »
Câu 7:
Cho tam giác ABC vuông tại A, gọi I là giao điểm các đường phân giác các góc trong của tam giác ABC, M là trung điểm BC.
a) Biết AB = 6 cm, AC = 8 cm. Tính .
Xem lời giải »
Câu 8:
b) Biết = 90°. Ba cạnh của tam giác ABC tỉ lệ với ba số nào?
Xem lời giải »