Cho tam giác ABC. Tìm điểm M thỏa mãn vecto MA + vecto MB + 2 vecto MC
Câu hỏi:
Cho tam giác ABC. Tìm điểm M thỏa mãn \[\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \]
A. M là trung điểm của cạnh IC, với I là trung điểm của AB.
B. M trùng với đỉnh C của ∆ABC.
C. M là trọng tâm của ∆ABC.
D. M là đỉnh của hình bình hành MCAB.
Trả lời:
Đáp án đúng là: A
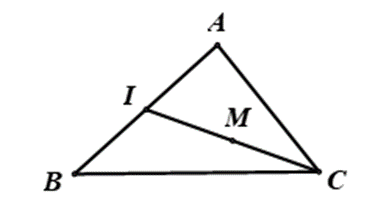
Gọi I là trung điểm của cạnh AB. Ta có:
\[\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \]
\[ \Leftrightarrow 2\overrightarrow {MI} + 2\overrightarrow {MC} = \overrightarrow 0 \]
\[ \Leftrightarrow 2\left( {\overrightarrow {MI} + \overrightarrow {MC} } \right) = \overrightarrow 0 \]
\[ \Leftrightarrow \overrightarrow {MI} + \overrightarrow {MC} = 0\]
Vậy M là trung điểm của IC.

