Cho tam giác ABC Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt
Câu hỏi:
Cho tam giác ABC Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm của DF và BC. Chứng minh \(\frac{{DM}}{{MF}} = \frac{{AC}}{{AB}}\).
Trả lời:
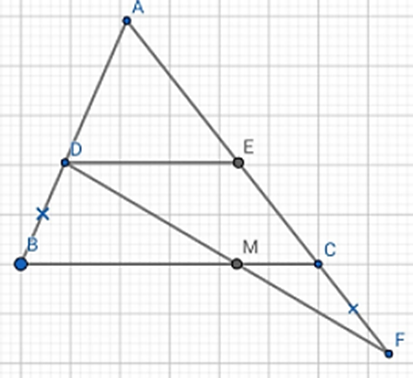
Xét ∆ABC có DE // BC
Áp dụng định lý Talet ta có: \(\frac{{AB}}{{CD}} = \frac{{AC}}{{CE}}\)
Suy ra: \(\frac{{CE}}{{BD}} = \frac{{AC}}{{AB}}\)
Vì CF = BD (giả thiết) nên \(\frac{{CE}}{{CF}} = \frac{{AC}}{{AB}}\)(1)
Xét ∆DEF có CM // DE (vì DE // BC)
Theo Talet ta có: \(\frac{{DM}}{{MF}} = \frac{{CE}}{{CF}}\) (2)
Từ (1) và (2) suy ra: \(\frac{{DM}}{{MF}} = \frac{{AC}}{{AB}}\).