Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D. a) Chứng minh BE = CD, AD = AE. b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứ

Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.

a) Chứng minh BE = CD, AD = AE.

b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh tam giác MAC vuông cân.

c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.

Lời giải

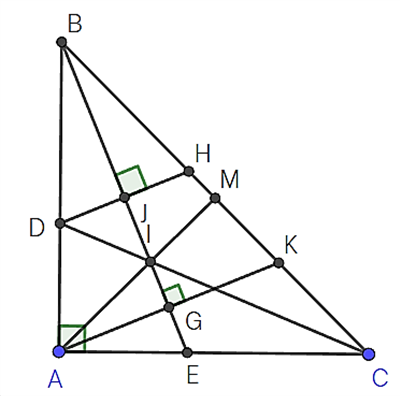
a) Do tam giác ABC vuông cân nên $\widehat {ABC} = \widehat {ACB} \Rightarrow \widehat {ABE} = \widehat {ACB}$

Xét tam giác vuông ABE và tam giác vuông ACD có:

AB = AC (gt)

$\widehat {ABE} = \widehat {ACB}$

Þ DABE = DACD (Cạnh góc vuông - góc nhọn kề)

Þ BE = CD; AE = AD

b) I là giao điểm của hai tia phân giác góc B và góc C của tam giác ABC nên AI cũng là phân giác góc A.

Do tam giác ABC cân tại A nên AI là phân giác đồng thời là đường cao và trung tuyến.

Vậy thì $\widehat {AMC} = 90^\circ ;\;BM = MC = AM$

Từ đó suy ra tam giác AMC vuông cân tại M.

c) Gọi giao điểm của DH, AK với BE lần lượt là J và G. 

Do DH và AK cùng vuông góc với BE nên ta có 

DBDJ = DBHJ; DBAG = DBKG Þ BD = BH; BA = BK

Þ HK = AD

Mà AD = AE nên HK = AE (1)

Do tam giác BAK cân tại B, có $\widehat B = 45^\circ \Rightarrow \widehat {BAK} = \frac{{180^\circ - 45^\circ }}{2} = 67,5^\circ$

$\Rightarrow \widehat {GAE} = 90^\circ - 67,5^\circ = 22,5^\circ = \frac{{\widehat {IAE}}}{2}$

Suy ra AG là phân giác góc IAE.

Từ đó ta có $\widehat {KAC} = \widehat {ICA} = 22,5^\circ$

Þ DAKC = DCIA (g - c - g) Þ KC = IA

Lại có tam giác AIE có AG là phân giác đồng thời đường cao nên nó là tam giác cân, hay AI = AE. Suy ra KC = AE (2)

Từ (1) và (2) suy ra HK = KC.