Cho tam giác ABC vuông tại A, BC = a căn bậc hai 3, M là trung điểm của BC
Câu hỏi:
Cho tam giác ABC vuông tại A, \(BC = a\sqrt 3 \), M là trung điểm của BC và có \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{a^2}}}{2}\). Tính cạnh AB, AC.
A. \[{\rm{A}}B = a,AC = a\sqrt 2 \]
B. \[{\rm{A}}B = a\sqrt 2 ,AC = a\sqrt 2 \]
C. \[{\rm{A}}B = a\sqrt 2 ,AC = a\]
D. \[{\rm{A}}B = a,AC = a\].
Trả lời:
Đáp án đúng là: A
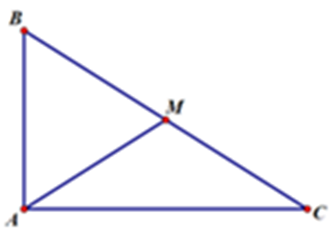
Ta có: \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{a^2}}}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )(\overrightarrow {AC} + \overrightarrow {AB} ) = \frac{{{a^2}}}{2}\\ \Leftrightarrow A{C^2} - A{B^2} = {a^2}\end{array}\)
Mặt khác, tam giác \({\rm{ABC}}\) vuông tại A nên \(A{B^2} + A{C^2} = 3{a^2}\)
Suy ra \(\left\{ {\begin{array}{*{20}{c}}{A{C^2} = 2{a^2}}\\{A{B^2} = {a^2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AC = a\sqrt 2 }\\{AB = a}\end{array}} \right.} \right.\)
Vậy ta chọn đáp án A.

![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
