Cho tam giác ABC vuông tại A có AC = 2AB. Vẽ tia phân giác Ax của A. Từ B vẽ đường thẳng vuông góc với Ax cắt AC tại F. Từ C vẽ đường thẳng vuông góc Ax cắt Ax tại E. a) Chứng minh rằng: Tứ g
Câu hỏi:
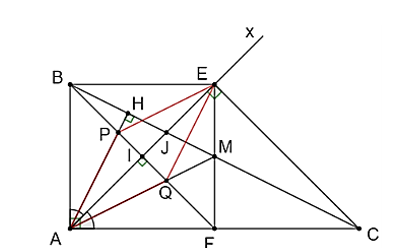
Cho tam giác ABC vuông tại A có AC = 2AB. Vẽ tia phân giác Ax của A. Từ B vẽ đường thẳng vuông góc với Ax cắt AC tại F. Từ C vẽ đường thẳng vuông góc Ax cắt Ax tại E.
a) Chứng minh rằng: Tứ giác ABEF có bốn cạnh bằng nhau.
Trả lời:
Lấy I là giao của Ax và BF.
a) AI là tia phân giác của góc BAF và AI cũng là đường cao của tam giác BAF nên
∆BAF cân tại A nên AB = AF.
Mà = 90°.
Khi đó ABEF là hình vuông.
Vậy ABEF có bốn cạnh bằng nhau.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm số tự nhiên a nhỏ nhất sao cho chia a cho 3; 5; 7 được số dư theo thứ tự là 2; 3; 4.
Xem lời giải »
Câu 2:
Tìm số tự nhiên có hai chữ số biết rằng khi chia số đó cho hiệu các chữ số của nó ra được thương là 28 và dư 1.
Xem lời giải »
Câu 5:
b) Chứng minh rằng: Tứ giác BECF là hình bình hành.
Xem lời giải »
Câu 6:
c) Vẽ trung tuyến AM và đường cao AH. BF cắt AH và AM tại P và Q. Hỏi APEQ là hình gì?
Xem lời giải »
Câu 7:
Chứng minh: n³ – 13n chia hết cho 6 (n thuộc ℤ).
Xem lời giải »
Câu 8:
Có bao nhiêu số tự nhiên gồm 6 chữ số khác nhau đôi một trong đó có mặt chữ số 0 nhưng không có mặt chữ số 1?
Xem lời giải »