Câu hỏi:
Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 6a; BC = 10a; với a là số thực dương.
1) Tính BH theo a.
2) Tính cos \(\widehat {ABC}\).
Trả lời:
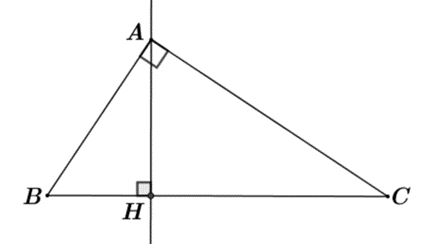
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
1) AB2 = BH.BC
⇒ (6a)2 = BH.10a
BH = 36a2 : 10a = 3,6a
2)\(\cos \widehat {ABC} = \frac{{BH}}{{AB}} = \frac{{3,6a}}{{6a}} = \frac{3}{5}\).
Câu 1:
Tính tích phân\(\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\sqrt {1 + \sin x} dx} \).
Câu 3:
Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right|;\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right|\).
Câu 4:
Cho tam giác đều cạnh a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|;\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Câu 5:
Cho tam giác ABC đều, cạnh a, tâm O. Tính \(\left| {\overrightarrow {AC} - \overrightarrow {AB} - \overrightarrow {OC} } \right|\).
Câu 6:
Cho hai số dương x;y thỏa mãn điều kiện x+y ≤ 1. Chứng minh: \({x^2} - \frac{3}{{4x}} - \frac{x}{y} \le \frac{{ - 9}}{4}\).
Câu 7:
Chọn ngẫu nhiên 3 số từ tập S = {1; 2; ...; 11}. Tính xác suất để tổng ba số được chọn là 12.
Câu 8:
Tính giá trị biểu thức sau : B = cos0° + cos20° + cos 40° + ... + cos160° + cos180°.
