Cho tam giác ABCΔABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE

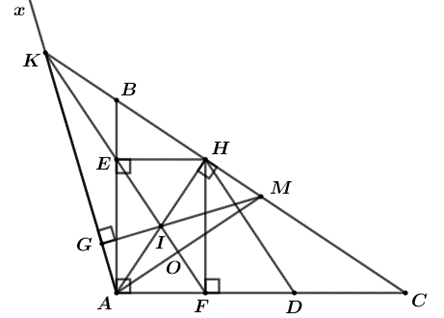
a) Chứng minh tứ giác AEHF là hình chữ nhật.

ΔABC vuông tại A ⇒ $\widehat {BAC}$= 90°

Vì HE⊥AB, HF⊥AC nên $\widehat {HEA}$= 90°, $\widehat {HFA}$= 90°

Xét tứ giác AEHF ta có:

$\widehat {HEA} = \widehat {HFA} = \widehat {EAF}$= 90°

Suy ra, tứ giác AEHF là hình chữ nhật (dấu hiệu nhận biết).

b) Gọi D là điểm đối xứng của A qua F.

Vì AEHF là hình chữ nhật suy ra EH // AF và EH = AF (tính chất của hình chữ nhật)

Vì D là tâm đối xứng của A qua F nên F là trung điểm của AD. Suy ra, AF = FD.

Do đó, EH // FD và EH = FD.

Suy ra, DHEF là hình bình hành (dấu hiệu nhận biết)

c)

+) Vì I là giao điểm của EF và AH nên ba điểm E, I, F thẳng hàng.

+) Gọi O là giao điểm của EF và AM.

Vì AM là đường trung tuyến của ΔABCΔABC nên AM = MC suy ra ΔAMC cân tại M. Do đó, $\widehat {MAC} = \widehat {MCA}$

Vì EHFA là hình chữ nhật, có I là giao điểm hai đường chéo nên ta có $\widehat {IAF} = \widehat {IFA}$

Xét ΔAHC ta có: $\widehat {HAC} + \widehat {HCA} = 90^\circ$ hay $\widehat {IAF} + \widehat {MCA} = 90^\circ$

⇒ $\widehat {IAF} + \widehat {MAC} = 90^\circ$ hay $\widehat {OAF} + \widehat {OFA} = 90^\circ$

Xét ΔOAF có: $\widehat {OAF} + \widehat {OFA} = 90^\circ$⇒ $\widehat {AOF} = 90^\circ$

⇒ EF vuông góc với AM tại O hay IF vuông góc với AM tại O.

+) Xét ΔKAM ta có:

GM ⊥ KA tại G

AH ⊥ KM tại H

Mà I là giao điểm của AH và GM nên I là trực tâm của ΔKAM.

⇒ KI ⊥ AM mà IF ⊥ AM

 ⇒ K, I, F thẳng hàng.

Ta có:

Ba điểm E, I, F thẳng hàng.

Ba điểm K, I, F thẳng hàng.

⇒ Bốn điểm I, K, E, F thẳng hàng.