Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt
Câu hỏi:
Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H (D Î BC, E Î AC, F Î AB). Chứng minh các tứ giác BDHF, BFEC nội tiếp.
Trả lời:
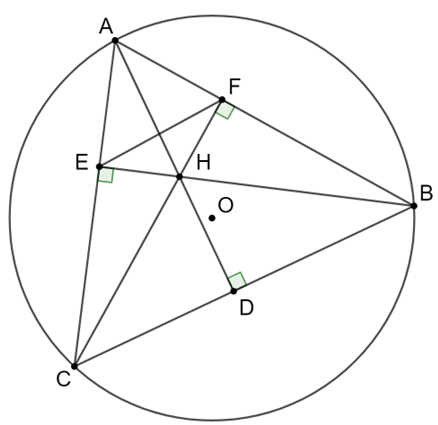
a) Ta có: \(AD \bot BC \Rightarrow \widehat {ADB} = 90^\circ \Rightarrow \widehat {HDB} = 90^\circ \) (1)
\(CF \bot AB \Rightarrow \widehat {CFB} = 90^\circ \Rightarrow \widehat {HFB} = 90^\circ \) (2)
Từ (1) và (2), ta thấy \(\widehat {HDB} + \widehat {HFB} = 90^\circ + 90^\circ = 180^\circ \)
Tứ giác BDHF có tổng hai góc đối bằng 180°.
Vậy tứ giác BDHF nội tiếp.
Ta có: \(BE \bot AC \Rightarrow \widehat {BEC} = 90^\circ \) (3)
\(CF \bot AB \Rightarrow \widehat {CFB} = 90^\circ \) (4)
Từ (3) và (4), ta thấy \(\widehat {BEC} = \widehat {CFB} = 90^\circ \).
Tứ giác BDHF có hai góc cùng chắn cung bằng nhau.
Vậy tứ giác BFCE nội tiếp.

