Có bao nhiêu số nguyên m thuộc đoạn để hàm số nghịch biến trên khoảng
Câu hỏi:
Cho hàm số liên tục trên R và có đạo hàm với mọi . Có bao nhiêu số nguyên m thuộc đoạn để hàm số nghịch biến trên khoảng ?
A. 2010
B. 2012
C. 2011
D. 2009
Trả lời:
Ta có:
Hàm số g (x) nghịch biến trên
(do )
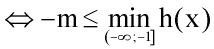
Ta có:
BBT:
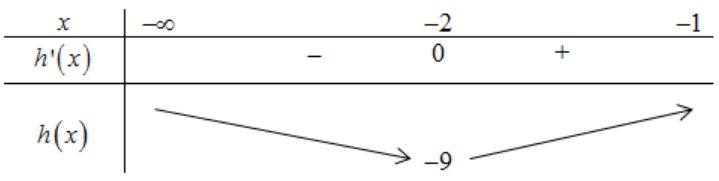
Dựa vào BBT ta có:
Mà và m nguyên nên hay có giá trị của m thỏa mãn.
Đáp án cần chọn là: C
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong tất cả các giá trị của tham số m để hàm số đồng biến trên R, giá trị nhỏ nhất của m là:
Xem lời giải »
Câu 2:
Tìm các giá trị của tham số m sao cho hàm số nghịch biến trên R?
Xem lời giải »
Câu 3:
Xác định giá trị của tham số m để hàm số nghịch biến trên khoảng (0;1)
Xem lời giải »
Câu 4:
Tìm m để hàm số nghịch biến trên khoảng
Xem lời giải »
Câu 5:
Cho hàm số y = f (x) có đạo hàm trên R và bảng xét dấu của đạo hàm như sau:

Có bao nhiêu số nguyên để hàm số nghịch biến trên khoảng ?
Xem lời giải »
Câu 6:
Cho hàm số f(x) có bảng xét dấu có đạo hàm như hình bên dưới:
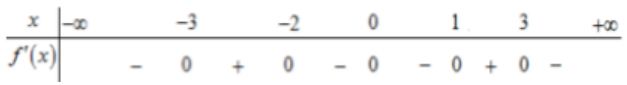
Hàm số đồng biến trên khoảng
Xem lời giải »
Câu 7:
Cho f (x) mà đồ thị hàm số y = f ' (x) như hình bên. Hàm số đồng biến trên khoảng?
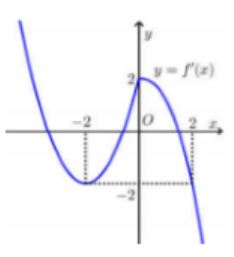
Xem lời giải »
Câu 8:
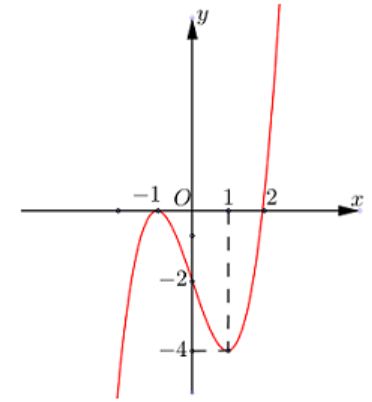
Cho hàm số f (x) có đạo hàm liên tục trên R và có đồ thị của hàm như hình vẽ. Xét hàm số . Mệnh đề nào dưới đây sai?
Xem lời giải »

