Gọi S là tập hợp tất cả các số nguyên dương của tham số m sao cho bất phương
Câu hỏi:
Gọi S là tập hợp tất cả các số nguyên dương của tham số m sao cho bất phương trình 4x – m . 2x – m + 15 ≥ 0 có nghiệm đúng với mọi x ∈ [1; 2]. Tính số phần tử của S.
A. 7
B. 4
C. 9
D. 6.
Trả lời:
Đáp án đúng là: D
4x – m . 2x – m + 15 ≥ 0 (1)
Đặt \({2^x} = t(t > 0)\) ta được \({t^2} - mt - m + 15 \ge 0\) (2)
Để bất phương trình (1) có nghiệm đúng với mọi x ∈ [1; 2] thì (2) đúng với mọi t ∈ [2; 4]
Ta có: \((2) \Leftrightarrow {t^2} + 15 \ge m(t + 1) \Leftrightarrow \frac{{{t^2} + 15}}{{t + 1}} \ge m\)
Xét hàm số \(f(t) = \frac{{{t^2} + 15}}{{t + 1}},t \in [2;4]\)
Ta có \(f'(t) = \frac{{(t + 5)(t - 3)}}{{{{(t + 1)}^2}}}\); \(f'(t) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = - 5\end{array} \right. \Leftrightarrow t = 3\)
Bảng biến thiên:
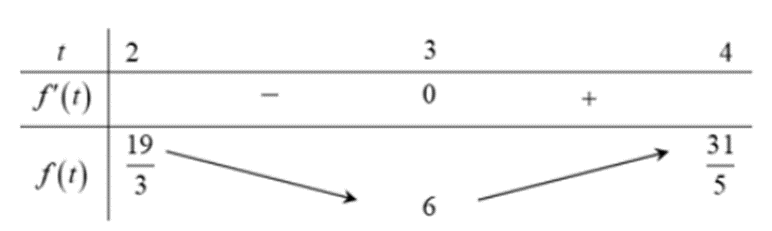
Suy ra m ≤ 6
Vậy ta chọn đáp án D.

![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
